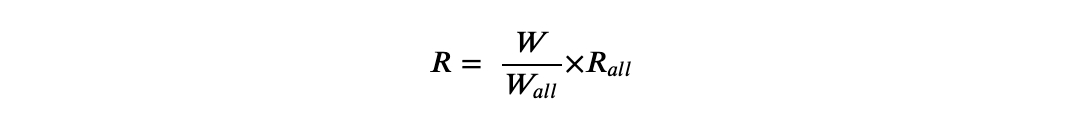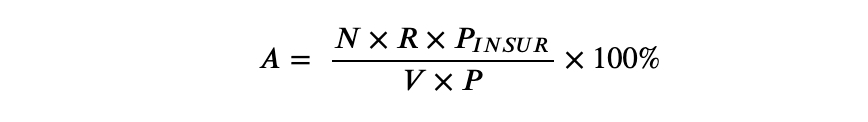Staking Mechanisms

Understanding the InsurAce protocol's staking mechanics.

Mining

Mining Pools

Mining pools are fundamental elements of the InsurAce protocol's mutual cover model. They act as liquidity reserves. InsurAce.io coverage capability is backed by substantial amounts of capital gathered in the mining pools.

InsurAce.io's mining pools are built based on the following considerations:

Asset Popularity
Asset Liquidity
Price Volatility

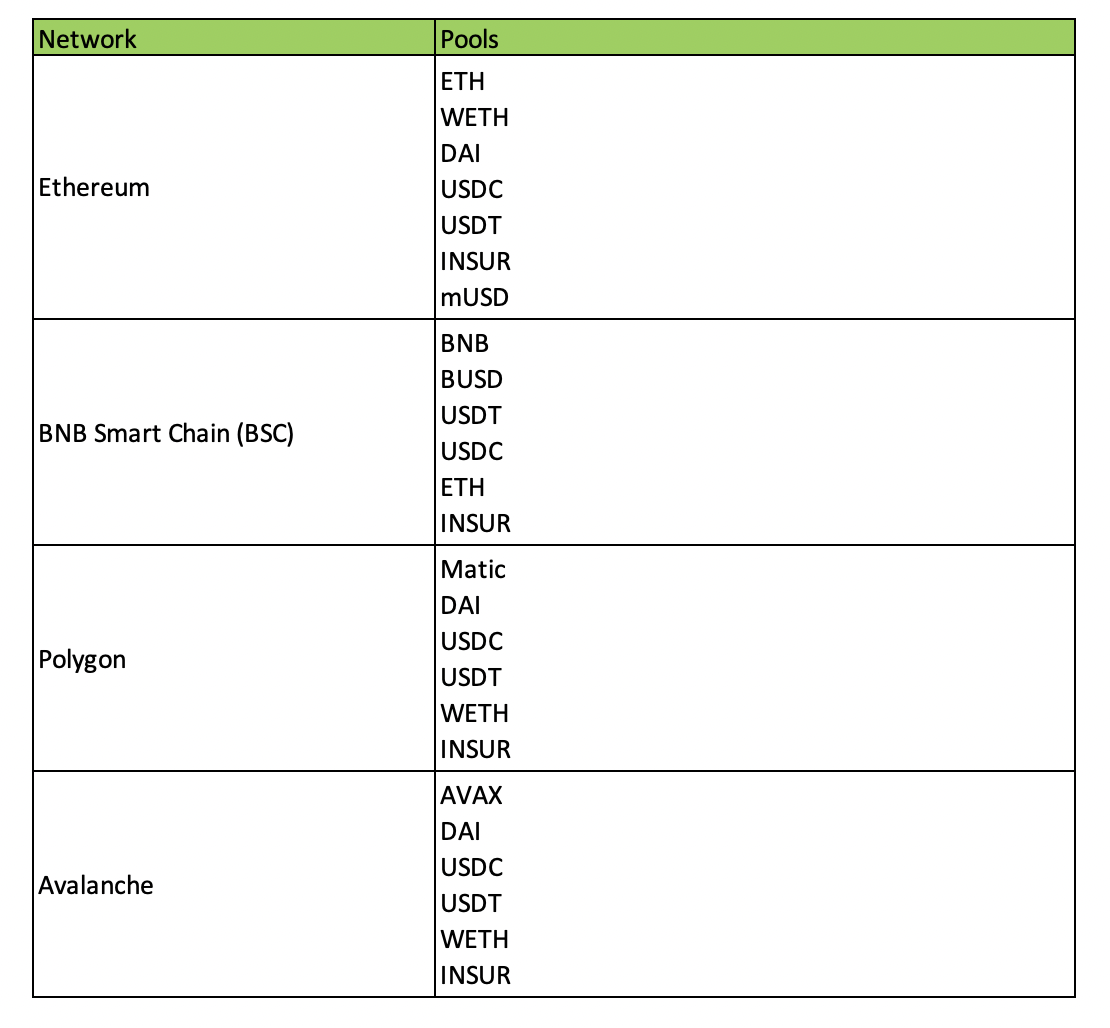
Currently, InsurAce.io supports the following mining pools:

New mining pools may be introduced based on market developments.

LPTokens

LPTokens are tokens used by stakers to prove ownership of their staked principal token (e.g. ETH/DAI) in mining pools. The following are important factors to consider with regards to LPTokens:

LPTokens are minted and attached to the staker's wallet as soon as the staker starts staking.
Once the staker withdraws the principal tokens (ETH/DAI) from the respective mining pool, their corresponding LPTokens are burned.
At the moment, LPTokens are non-transferable, non-exchangeable and cannot be staked on other platforms.
It is important not to lose LPTokens in order to avoid losing access to the principal tokens in the mining pool.

Mining Pool Factor

LPTokens are minted based on the mining pool's factor, $μ$ :

μ_t = \frac {LPToken_t} {Principal_t}

where

$t$ is the principal token of the pool
${Principal_t}$ is the remaining principal token in the pool
$LPToken_t$ is the remaining LPToken in the pool

In other words, $μ_t$ is the amount of $LPToken_t$ you will get when you stake 1 Token $t$ .

LPToken Minting

The formula for LPTokens minting is

\Delta{LPToken}_t = μ_t \times{Stake_t}

where

$t$ is the principal token of the pool
$Stake_t$ is the amount of principal token staked by end-users
$\Delta{LPToken}_t$ is the Amount of LPTokens $t$ to be minted

Example

A staker staked 10 ETH in the mining pool. The ETH pool's factor $μ_{ETH}$ is 1 at that moment. The amount of $LPToken_{ETH}$ he will get is

\Delta{LPToken}_{ETH} = μ_{ETH} \times Stake_{ETH} = 1 \times 10 = 10

Rewards

Staking is a key element of InsurAce.io. $INSUR tokens / governance power is rewarded to all stakers to incentivize staking:

$INSUR Distribution Formula for staking

$INSUR rewards are calculated based on the following formula

Rewards = \displaystyle\sum_{t=0}^T ( \frac {X \times Y \times N \times K} {Z \times J})

where

X = INSUR Released Per Block
Y = Token Pool Weightage
Z = Total Pools Weightage
K = Amount of $LPToken_t$ staker holding
J = Total Supply of $LPToken_t$
N = Number of Blocks between events
T = Sequence of Stake or Withdraw Happened

To better understand the above formula, let's assume the following:

Two Token Pools, one is ETH, the other one is DAI
Weightage for each pool is 50:50
Per block, we release 2 INSUR token
UserA stakes in 1 ETH in block 1
UserB stakes in 1 ETH in block 10

Some calculations:

For ETH pool, the $INSUR released per block will be (2 * 50)/(50 + 50) = 1 $INSUR
From block 1 to block 10, only UserA staked here, so the reward for him is (10 - 1)*1*1/1 = 9.
From block 10 onwards, UserB also joins the party, therefore these two will share the $INSUR emitted per block.
1. For UserA, reward per block is 1*1/(1+1) = 0.5
2. For UserB, reward per block is 1*1/(1+1) = 0.5

The more blocks a staker has staked for, the more $INSUR tokens rewarded to the staker.

APY Calculation

Step 1: Calculate the rewards per block

where

R = The reward per block of the mining pool (in INSUR)
$R_{all}$ = The total reward for all mining pools (in INSUR), obtained from the rewardPerBlock function in StakersPool contract.
W = The weight of the mining pool, obtained from the poolWeightPT function in StakersPool contract.
$W_{all}$ = The sum of the weights of all mining pools, obtained from the totalPoolWeight function in StakersPool contract.

Step 2: Calculate the mining pool's APY

where

A = The APY of the mining pool
N = The number of blocks mined in a year. For the Ethereum blockchain, this is set to the number of seconds in a year / average block time = 365 x 24 x 60 x 60 / 15 = 2102400.
R = The reward per block of the mining pool (in INSUR), obtained from step 1.
$P_{INSUR}$ = The price of INSUR (in USDC), can be obtained from any price provider.
V = The total value locked in a mining pool, obtained from the stakedAmountPT function in StakersPool contract.
P = The price of the token of the mining pool (in USDC), can be obtained from any price provider.

Example

Before calculating the APY of the INSUR mining pool, staking data (by querying the blockchain) and token prices are required.

The StakersPool contract (address: 0x136D841d4beCe3Fc0E4dEbb94356D8b6B4b93209) has functions that provide the required staking data.

function rewardPerBlock() view returns (uint256) : We can get $R_{all}$ by calling this function.
function totalPoolWeight() view returns (uint256) : We can get $W_{all}$ by calling this function.
function poolWeightPT(address lpToken) view returns (uint256) : We can get W by calling this function with the “lpToken” parameter set to the LPTokenINSUR token address (0x7e68521a2814a84868Da716b9f436b53e6764C1D).
function stakedAmountPT(address token) view returns (uint256) : We can get V by calling this function with the “token” parameter set to the INSUR token address (0x544c42fBB96B39B21DF61cf322b5EDC285EE7429).

Token prices can be obtained and verified through price providers, such as 1inch, CoinGecko etc. Of particular interest are the following:

$P_{INSUR}$ – The price of INSUR in USDC
P – The price of the token of the mining pool in USDC (in this example, this happens to be the same as $P_{INSUR}$ )

After getting all the data, the APY of the INSUR mining pool is calculated as follows:

Reference

Tokens

The contract address for the mining tokens and LP tokens can be found below:

pageSmart Contract Addresses

Contract

StakersPool

Address: 0x136D841d4beCe3Fc0E4dEbb94356D8b6B4b93209

Additional topic

Rounding Loss

Rounding loss, albeit negligible, may occur when dividing results in infinite decimals due to smart contract limitations on precision.

Take the ETH Pool for example. Suppose that there are 9000 ETH in the ETH Pool, 10000 LPTokenETH is minted, and the staker plans to stake another 10 ETH, the minted LPTokenETH will be 11.111111111111111111.

\Delta{LPToken}_{ETH} = \frac {Principal_{ETH} \times Stake_{ETH}} {LPToken_{ETH}}

= \frac {10 \times 10000} {9000} = 11.1111111111111111

Based on the above formula, the amount of ETH which the staker can claim back is (excluding withdrawal fees, etc.):

\Delta{Unstake}_{ETH} = \frac {\Delta{LPToken_{ETH}} \times Principal_{ETH}} {LPToken_{ETH}}

= \frac {11.111111111111111111 * 9000} {10000} = 9.99999999999999999

The rounding loss is $1/10^{17}$ ETH which is negligible.

Events impacting Capital Pool Factor

At the start of any capital pool, the capital pool's factor equals one (1). It stays constant until events have changed the ratio between the principal token and the LPToken.

For example, a Claim Payout is an event which will change said ratio since mining pools share a portion of Claim Payouts. Besides having the right to earn rewards from InsurAce protocol, stakers also bear the responsibility for making Claim Payouts. As a result, less principal than initially provided may be returned to stakers upon unstaking their capital from the InsurAce protocol.

PreviousMining NextStaking Risks

Last updated 1 year ago